Реактивное сопротивление в электротехнике
Известный в электротехнике закон Ома объясняет, что если по концам какого-то участка цепи приложить разность потенциалов, то под ее действием потечет электрический ток, сила которого зависит от сопротивления среды.
Источники переменного напряжения создают ток в подключенной к ним схеме, который может повторять форму синусоиды источника или быть сдвинутым по углу от него вперед либо назад.
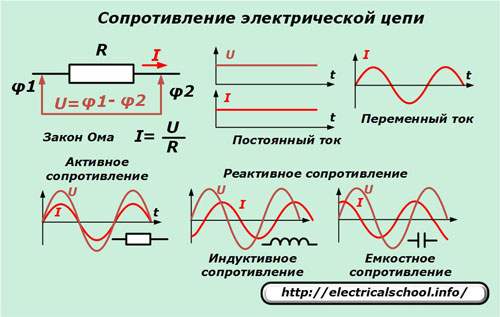
Если электрическая цепь не изменяет направления прохождения тока и его вектор по фазе полностью совпадает с приложенным напряжением, то такой участок обладает чистым активным сопротивлением. Когда же наблюдается отличие во вращении векторов, то говорят о реактивном характере сопротивления.
Различные электротехнические элементы обладают неодинаковой способностью отклонять направление тока, протекающего через них и изменять его величину.
Реактивное сопротивление катушки
Возьмем источник стабилизированного переменного напряжения и отрезок длинной изолированной проволоки. Вначале подключим генератор на всю расправленную проволоку, а затем на ее же, но смотанную кольцами вокруг магнитопровода, который используется для улучшения прохождения магнитных потоков.
Точно замеряя в обоих случаях ток, можно заметить, что при втором эксперименте будет замечено значительное снижение его величины и отставание по фазе на определенный угол.
Это происходит за счет возникновения противодействующих сил индукции, проявляющихся под действием закона Ленца.
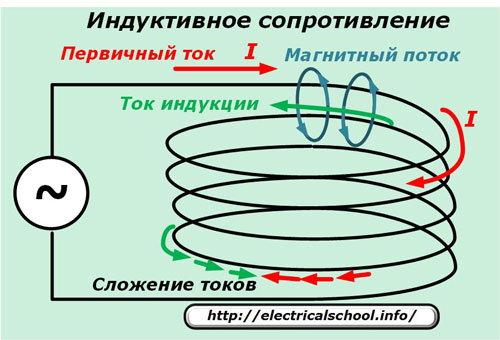
На рисунке прохождение первичного тока показано красными стрелками, а создаваемое им магнитное поле — синими. Направление его движения определяется по правилу правой руки. Оно же пересекает все соседние витки внутри обмотки и индуцирует в них ток, показанный зелеными стрелками, который ослабляет величину приложенного первичного тока, одновременно сдвигая его направление по отношению к приложенной ЭДС.
Чем большее число витков намотано на катушке, тем сильнее создается индуктивное сопротивление XL, уменьшающее первичный ток.
Его величина зависит от частоты f, индуктивности L, рассчитывается по формуле:
За счет преодоления сил индуктивности ток на катушке отстает от напряжения на 90 градусов.
Реактивное сопротивление трансформатора
У этого устройства на общем магнитопроводе расположены две или большее количество обмоток. Одна из них получает электроэнергию от внешнего источника, а другим она передается по принципу трансформации.
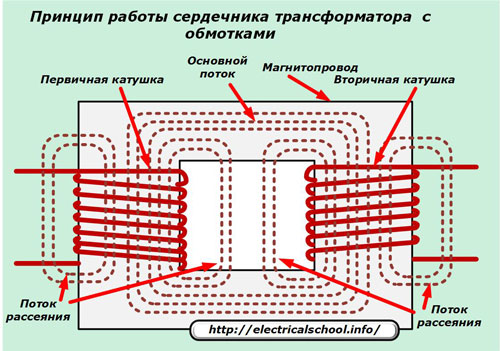
Первичный ток, проходящий по силовой катушке, наводит в магнитопроводе и вокруг него магнитный поток, который пересекает витки вторичной обмотки и формирует в ней вторичный ток.
Поскольку идеально создать конструкцию трансформатора невозможно, то часть магнитного потока будет рассеиваться в окружающую среду и создаст потери. Они называются потоком рассеивания и влияют на величину реактивного сопротивления рассеяния.
К ним добавляется активная составляющая сопротивления каждой обмотки. Полученная суммарная величина называется электрическим импедансом трансформатора или его комплексным сопротивлением Z, создающим перепады напряжения на всех обмотках.
Для математического выражения взаимосвязей внутри трансформатора активное сопротивление обмоток (обычно изготавливаемых из меди) обозначают индексами «R1» и «R2», а индуктивное — «Х1» и «Х2».
Импеданс в каждой обмотке имеет вид:
В этом выражении индексом «j» обозначена мнимая единица, расположенная на вертикальной оси комплексной плоскости.
Наиболее критичный режим в отношении индуктивного сопротивления и возникновении реактивной составляющей мощности создается при параллельном подключении трансформаторов в работу.
Реактивное сопротивление конденсатора
Конструктивно в его состав входят две или несколько токопроводящих пластин, отделенных слоем материала, обладающего диэлектрическими свойствами. За счет этого разделения постоянный ток не может пройти через конденсатор, а переменный — способен, но с отклонением от первоначальной величины.
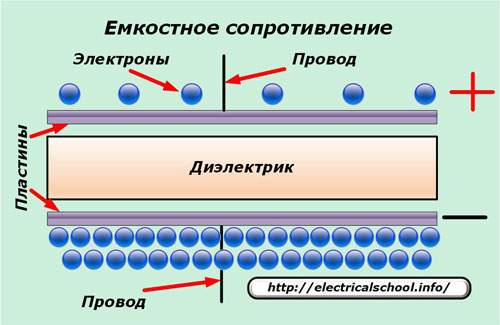
Ее изменение объясняется принципом работы реактивного — емкостного сопротивления.
Под действием приложенного переменного напряжения, изменяющегося по синусоидальной форме, на обкладках происходит всплеск, накопление зарядов электрической энергии противоположных знаков. Общее их количество ограничено габаритами устройства и характеризуется емкостью. Чем она больше, тем дольше времени идет заряд.
В течение следующего полупериода колебания полярность напряжения на обкладках конденсатора меняется на противоположное. Под его воздействием происходит смена потенциалов, перезарядка сформированных зарядов пластин. Таким способом создается протекание первичного тока и противодействие его прохождению, когда он уменьшается по величине и сдвигается по углу.
По этому вопросу у электриков есть шутка. Постоянный ток на графике представлен прямой линией и когда он идет по проводу, то электрический заряд, дойдя до обкладки конденсатора упирается в диэлектрик, попадая в тупик. Эта преграда не дает ему пройти.
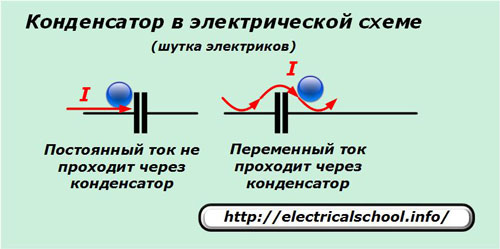
Синусоидальная же гармоника идет переваливаясь через препятствия и заряд, свободно перекатившись через нарисованные обкладки, теряет небольшую часть энергии, которая зацепилась за пластины.
У этой шутки есть скрытый смысл: при подаче на обкладки постоянного или выпрямленного пульсирующего напряжения между пластинами за счет накопления ими электрических зарядов создается строго постоянная разность потенциалов, которая сглаживает все скачки питающей цепи. Это свойство конденсатора увеличенной емкости используется в стабилизаторах постоянного напряжения.
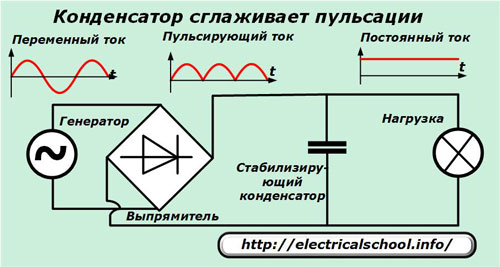
В общем, емкостное сопротивление Xc или противодействие прохождению через него переменному току зависит от конструкции конденсатора, определяющей емкость «С», и выражается формулой:
Хс = 1/2 π fC = 1/ω C
За счет перезарядки обкладок ток через конденсатор опережает напряжение на 90 градусов.
Реактивное сопротивление линии электропередачи
Любая ЛЭП создается для передачи электрической энергии. Ее принято представлять участками со схемами замещения, обладающими распределенными параметрами активного r, реактивного (индуктивного) x сопротивления и проводимости g, отнесенными к единице длины, как правило, одному километру.
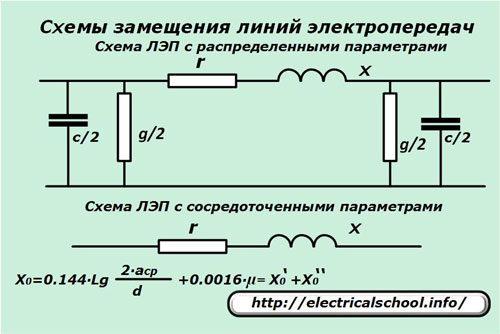
Если пренебречь влиянием емкости и проводимости, то можно пользоваться упрощенной схемой замещения линии, обладающей сосредоточенными параметрами.
Передача электроэнергии по неизолированным проводам, расположенным на открытом воздухе, требует значительного удаления их между собой и от земли.

При этом индуктивное сопротивление одного километра провода трехфазной линии можно представить выражением Х0. Оно зависит от:
среднего удаления осей проводов между собой аср;
наружного диаметра фазных жил d;
относительной магнитной проницаемости материала µ;
внешнего индуктивного сопротивления линии Х0’;
внутреннего индуктивного сопротивления линии Х0’’.
Для справки: индуктивное сопротивление 1 км ВЛ, выполненной из цветного металла составляет порядка 0,33÷0,42 Ом/км.
Линия электропередачи, использующая высоковольтный кабель, конструктивно отличается от ВЛ. У нее расстояние между фазами проводов значительно уменьшено и определяется толщиной слоя внутренней изоляции.

Такой трехжильный кабель можно представить в виде конденсатора с тремя обкладками из жил, протянутых на большое расстояние. С увеличением его протяженности возрастает емкость, снижается емкостное сопротивление и увеличивается емкостной ток, замыкающийся по кабелю.
В кабельных линиях под воздействием емкостных токов наиболее часто происходят однофазные замыкания на землю. Для их компенсации в сетях 6÷35 кВ используют дугогасящие реакторы (ДГР), которые подключают через заземленную нейтраль сети. Их параметры подбираются сложными методами теоретических расчетов.
Старые ДГР не всегда эффективно работали из-за низкого качества настройки и несовершенства конструкции. Они создавались под усредненные расчетные токи замыканий, которые часто отличались от реальных значений.
Сейчас внедряются новые разработки ДГР, способные в автоматическом режиме отслеживать аварийные ситуации, быстро замерять их основные параметры и подстраиваться для надежного гашения токов замыкания на землю с точностью до 2%. Благодаря этому эффективность работы ДГР сразу возросла на 50%.
Принцип компенсации реактивной составляющей мощности конденсаторными установками
Электрические сети передают высоковольтную электроэнергию на огромные расстояния. Большинством ее потребителей являются электродвигатели, обладающие индуктивным сопротивлением, и резистивные элементы. Полная мощность, направляемая потребителям, состоит из активной составляющей Р, расходуемой на совершение полезной работы, и реактивной Q — вызывающей нагрев обмоток трансформаторов и электродвигателей.
Реактивная составляющая Q, возникая на индуктивных сопротивлениях, снижает качество электроэнергии. Для уничтожения ее вредного воздействия в восьмидесятых годах прошлого века в энергосистеме СССР использовалась схема компенсации за счет подключения конденсаторных батарей, обладающих емкостным сопротивлением, которое снижало косинус угла φ.
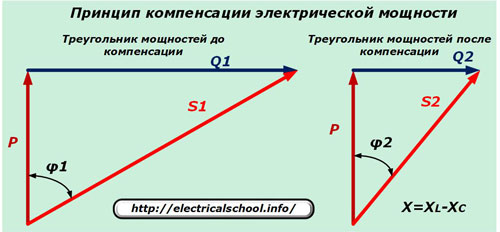
Они устанавливались на подстанциях, непосредственно питающих проблемных потребителей. Этим обеспечивалось местное регулирование качества электроэнергии.
Таким способом можно значительно уменьшить нагрузку на оборудование за счет снижения реактивной составляющей при передаче одной и той же активной мощности. Этот способ считается наиболее эффективным приемом энергосбережения не только на промышленных предприятиях, но и на объектах ЖКХ. Его грамотное использование позволяет значительно повысить надежность эксплуатации энергосистем.
Реактивное и активное сопротивление
Сопротивлением в электротехнике называют такую величину, которая характеризует противодействие отдельность части электрической сети или ее элементов электрическому току. Это основано на том, что сопротивление изменяет электрическую энергию и конвертирует ее в другие типы. Например, в сетях с переменных электротоком происходят необратимые изменения энергии и ее передача между участниками этой электроцепи.
Сопротивление как физическую величину трудно переоценить, так как она является одной из ключевых характеристик электричества в сети и прямо или пропорционально определяет силу тока и напряжение. Этот материал познакомит с такими понятиями как: активное сопротивление и реактивное сопротивление в цепи переменного тока, как проявляется зависимость активного сопротивления от частоты.

Какое сопротивление называется реактивным, какое активным
Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.

Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.

Какие отличия
Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть.
Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.

От чего зависит активное сопротивление
Активное электросопротивление зависит от сечения проводника. Это значит, что полезным сечением при электротоке с высокой частотой будет только тонкий наружный слой проводника. Из этого исходит также то, что активностное электросопротивление только возрастает с увеличением частоты электротока переменного типа.
Для того чтобы уменьшить поверхностный эффект проводника, по которому течет электроток высокой частоты, его изготавливают трубчатым и покрывают напылением металла, хорошо проводящего электрический ток, например, серебром.

В чем измеряется реактивное сопротивление
Само по себе, явление реактанса характерно только для цепей с электрическим током переменного типа. Обозначается оно латинской буквой «X» и измеряется в Омах. В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения. Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.
Важно! Абсолютно чистое реактивное электросопротивление имеет сдвиг фазы на ± 180/2. То есть, фаза «двигается» на π/2.

Как правильно измерять сопротивление
При работе с радиоаппаратурой иногда требуется измерять не только активностное, но и реактивное электросопротивление (индуктивность и емкость). Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.

Косвенный метод наиболее прост в своей реализации, так как не требует дополнительных схем включения. Одна требуется наличие трех отдельных приборов: амперметра, вольтметра и ваттметра. Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².

Области проявления
Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.
Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.
Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.
Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.

Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.
Определение импеданса сухого трансформатора – Трансформеры – 2020
Диагностика силового трансформатора (Январь 2020).

Определение сухого трансформатора Пропорциональное сопротивление (на фото сухого трансформатора фирмы Engineering B & S, Украина)
Введение
Процентное сопротивление представляет собой процентное напряжение, необходимое для циркуляции номинального тока через одну обмотку трансформатора, когда другая обмотка коротко замыкается на номинальном напряжении на номинальной частоте.
% Z относится к мощности короткого замыкания трансформатора во время условий короткого замыкания.
Для двух обмоточного трансформатора с импедансом 5% для намотки высокого напряжения потребуется 5% входного напряжения для наведения 100% номинального тока на вторичную обмотку при коротком замыкании вторичной обмотки.
Если к высоковольтной обмотке применено 100% номинальное напряжение, то во вторичной обмотке будет протекать приблизительно 20- кратный номинальный ток при коротком замыкании вторичной обмотки.
Уровни импеданса
| КВА | Минимальный импеданс, % |
| 0 – 150 | Стандарт производителя |
| 151 – 300 | 4 |
| 301 – 600 | 5 |
| 601 – 2, 500 | 6 |
| 2, 501-5, 000 | 6, 5 |
| 5 001 – 7 500 | 7, 5 |
| 7, 501 – 10, 000 | 8, 5 |
| Выше 10 000 | 9, 5 |
Важные заметки
- Сопротивление двухмоторного трансформатора не должно изменяться от гарантированного значения более чем на ± 7, 5%
- Сопротивление трансформатора, имеющего три или более обмотки или имеющих зигзагообразные обмотки, не может изменяться от гарантированного значения более чем на ± 10%
- Импеданс автотрансформатора не должен изменяться от гарантированного значения более чем на ± 10%
- Разность импедансов между трансформаторами той же конструкции не должна превышать 10% от гарантированных значений
- Разница импеданса между автоматическими трансформаторами той же конструкции не должна превышать 10% от гарантированных значений
Импеданс против процентного импеданса
Импеданс определяется в стандартном справочнике для инженеров-электриков как « кажущееся сопротивление цепи переменного тока или пути
векторная сумма сопротивления и реактивности пути ». Импеданс может состоять из сопротивления, емкостного реактивного сопротивления и индуктивного сопротивления и выражается в омах.
С точки зрения нагрузки общий входной импеданс может включать в себя сопротивление восходящего генератора, трансформатора, линейного реактора и проводников.
Сопротивление силовой системы полезно для оценки имеющегося тока короткого замыкания.
Примеры расчетов для трехфазного трансформатора мощностью 500 кВА, 4160: 480, 60 Гц, импеданса 6%:
Реактивное сопротивление трансформатора X t = (кВ 2 / МВА) x% Z / 100 = (0, 48 2 / 0, 5) x 0, 06 = 0, 027648 Ом
Приблизительный ток короткого замыкания = 480 / (1.732 x 0.027648) = 10 023, 7 А
Эффективное процентное сопротивление
Эффективный импеданс – это относительный импеданс реактора или трансформатора в реальных условиях эксплуатации. Поскольку нагрузки меньшего (кВА) имеют более высокий импеданс и, следовательно, потребляют меньший ток, чем большие (кВА) нагрузки, внутренние омы реактора или трансформатора представляют меньший процент импеданса нагрузки для небольшой нагрузки (кВА), чем для большой нагрузки.
Значение в омах приведет к снижению падения напряжения при протекании менее реактора или тока трансформатора. Если нагрузка составляет только половину номинального тока, то падение напряжения на импедансе будет на одну половину от номинального падения напряжения.
Примеры расчетов для трехфазного трансформатора мощностью 500 кВА, 4160: 480, 60 Гц, импеданса 6%:
Реактивное сопротивление трансформатора X t = (кВ 2 / МВА) x% Z / 100 = (0, 48 2 / 0, 5) x 0, 06 = 0, 027648 Ом
Номинальный вторичный ток = 500 000 / (480 x 1, 732) = 601, 4 А
Фактический ток нагрузки = 300 А
Падение напряжения при фактической нагрузке = 300 x 1.732 x 0.027648 = 14.36 вольт (14.36 / 480 = 0.0299 или 3% от 480 вольт )
Эффективный процентный импеданс = 6% x (300 / 601, 4) = 2, 99%
Сопротивление трансформатора (VIDEO)
Не могу посмотреть это видео? Нажмите здесь, чтобы посмотреть его на Youtube.
Ресурс: Курс ввода подстанции – Трансформатор сухого типа
Что такое реактивное сопротивление трансформатора?
Мы привыкли считать, что все магнитные потоки в трансформаторе пронизывают обе обмотки и магнитопровод. Если бы существовал идеальный трансформатор, то это действительно так бы и происходило. К сожалению, в реальности часть магнитного потока преодолевает изоляционное пространство, выходит за пределы обмоток и замыкается в них (см. рис. 1). В результате возникает реактивное сопротивление трансформатора. Такое явление ещё называют рассеиванием магнитных потоков.
 Рис. 1. Схема, иллюстрирующая рассеивание магнитных потоков
Рис. 1. Схема, иллюстрирующая рассеивание магнитных потоков
В катушках существуют и другие сопротивления, являющиеся причинами потерь мощности. Таковыми являются: внутреннее сопротивление материалов обмоток, и рассеивания, вызванные индуктивными сопротивлениями. Совокупность рассеиваний магнитных потоков называют внутренним сопротивлением или импедансом трансформатора.
Потери реактивных мощностей
Вспомним, как работает идеальный двухобмоточный трансформатор (см. рис. 2). Когда первичная обмотка окажется под переменным напряжением (например, от электрической сети), возникнет магнитный поток, который пронизывает вторичную катушку индуктивности. Под действием магнитных полей происходит возбуждение вторичных обмоток, в витках которых возникает ЭДС. При подключении активной мощности к прибору во вторичной цепи начинает протекать переменный ток с частотой входного тока.
 Рис. 2. Устройство трансформатора
Рис. 2. Устройство трансформатора
В идеальном трансформаторе образуется прямо пропорциональная связь между напряжениями в обмотках. Их соотношение определяется соотношением числа витков каждой из катушек. Если U1 и U2 – напряжения в первой и второй обмотке соответственно, а w1 и w2 – количество витков обмоток, то справедлива формула: U1 / U2 = w1 / w2.
Другими словами: напряжение в рабочей обмотке во столько раз больше (меньше), во сколько раз количество мотков второй катушки увеличено (уменьшено) по отношению к числу витков, образующих первичную обмотку.
Величину w1 / w2 = k принято называть коэффициентом трансформации. Заметим, что формула, приведённая выше, применима также для автотрансформаторов.
В реальном трансформаторе часть энергии теряется из-за рассеяния магнитных потоков (см. рис. 1). Зоны, где происходит концентрация потоков рассеяния обозначены пунктирными линиями. На рисунке видно, что индуктивность рассеяния охватывает магнитопровод и выходит за пределы обмоток.
Наличие реактивных сопротивлений в совокупности с активным сопротивлением обмоток приводят к нагреванию конструкции. То есть, при расчётах КПД необходимо учитывать импеданс трансформатора.
Обозначим активное сопротивление обмоток символами R1 и R2 соответственно, а реактивное – буквами X1 и X2. Тогда импеданс первичной обмотки можно записать в виде: Z1= R1+jX1. Для рабочей катушки соответственно будем иметь: Z2= R2+jX2, где j – коэффициент, зависящий от типа сердечника.
Реактивное сопротивление можно представить в виде разницы индукционного и ёмкостного показателя: X = RL – RC. Учитывая, что RL = ωL, а RC = 1/ωC, где ω – частота тока, получаем формулу для вычисления реактивного сопротивления: X = ωL – 1/ωC.
Не прибегая к цепочке преобразований, приведём готовую формулу для расчёта полного сопротивления, то есть, для определения импеданса трансформатора:

Суммарное сопротивление трансформатора необходимо знать для определения его КПД. Величины потерь в основном зависят от материала обмоток и конструктивных особенностей трансформаторного железа. Вихревые потоки в монолитных стальных сердечниках значительно больше, чем многосекционных конструкциях магнитопроводов. Поэтому на практике сердечники изготавливаются из тонких пластин трансформаторной стали. С целью повышения удельного сопротивления материала, в железо добавляют кремний, а сами пластины покрывают изоляционным лаком.
Для определения параметров трансформаторов важно найти активное и реактивное сопротивление, провести расчёты потерь холостого хода. Приведённая выше формула не практична для вычисления импеданса по причине сложности измерений величин индукционного и ёмкостного сопротивлений. Поэтому на практике пользуются другими методами для расчёта, основанными на особенностях режимов работы силовых трансформаторов.
Режимы работы
Двухобмоточный трансформатор способен работать в одном из трёх режимов:
- вхолостую;
- в режиме нагрузки;
- в состоянии короткого замыкания.
Для проведения расчётов режимов электрических цепей проводимости заменяют нагрузкой, величина которой равна потерям при работе в режиме холостого хода. Вычисления параметров схемы замещения проводят опытным путём, переводя трансформатор в один из возможных режимов: холостого хода, либо в состояние короткого замыкания. Таким способом можно определить:
- уровень потерь активной мощности при работе на холостом ходу;
- величины потерь активной мощности в короткозамкнутом приборе;
- напряжение короткого замыкания;
- силу тока холостого хода;
- активное и реактивное сопротивление в короткозамкнутом трансформаторе.
Параметры режима холостого хода
Для перехода в работу на холостом ходу необходимо убрать отсутствует нагрузку на вторичной обмотке, то есть – разомкнуть электрическую цепь. В разомкнутой катушке напряжение отсутствует. Главной составляющей тока в первичной цепи является ток, возникающий на реактивных сопротивлениях. С помощью измерительных приборов довольно просто найти основные параметры переменного тока намагничивания, используя которые можно вычислить потери мощности, умножив силу тока на подаваемое напряжение.
Схема измерений на холостом ходу показана на рисунке 3. На схеме показаны точки для подключения измерительных приборов.
 Рис. 3. Схема режима холостого хода
Рис. 3. Схема режима холостого хода
Формула, применяемая для расчётов параметров реактивной проводимости, выглядит так: Вт = Iх%*Sном / 100* Uв ном 2 Умножитель 100 в знаменателе применён потому, что величина тока холостого хода Iх обычно выражается в процентах.
Режим короткого замыкания
Для перевода трансформатора на работу в режиме короткого замыкания закорачивают обмотку низшего напряжения. На вторую катушку подают такое напряжение, при котором в каждой обмотке циркулирует номинальный ток. Поскольку подаваемое напряжение существенно ниже номинальных напряжений, то потери активной мощности в проводимости настолько малы, что ими можно пренебречь.
Таким образом, у нас остаются активные мощности в трансформаторе, которые расходуются на нагрев обмоток: ΔPk = 3* I1ном * Rт. Выразив ток I1 ном через напряжение Uка и сопротивление Rт, умножив выражение на 100, получим формулу для вычисления падения напряжения в зонах активного сопротивления (в процентах):

Активное сопротивление двухобмоточного силового трансформатора вычисляем по формуле:

Подставив значение Rт в предыдущую формулу, получим:

Вывод: в короткозамкнутом трансформаторе падение напряжения в зоне активного сопротивления (выраженная в %) прямо пропорционально размеру потерь активной мощности.
Формула для вычисления падения напряжения в зонах реактивных сопротивлений имеет вид:

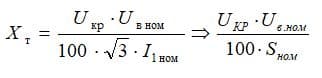
Величины реактивных сопротивлений в современных трансформаторах гораздо меньше активного. Поэтому можно считать что падение напряжения в зоне реактивного сопротивления Uк р ≈ Uк, поэтому для практических расчётов можно пользоваться формулой: XT = Uk*Uв ном 2 / 100*Sном
Рассуждения, приведённые выше, справедливы также для многообмоточных, в том числе и для трёхфазных трансформаторов. Однако вычисления проводятся по каждой обмотке в отдельности, а задача сводится к решению систем уравнений.
Знание коэффициентов мощности, сопротивления рассеивания и других параметров магнитных цепей позволяет делать расчёты для определения величин номинальных нагрузок. Это, в свою очередь, обеспечивает работу трансформатора в промежутке номинальных мощностей.
Реактивное сопротивление XL и XC
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении – положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток  .
.
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока  со сдвигом от функции напряжения на угол π/2 (90°).
со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать  .
.
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.
Реактивное сопротивление конденсатора.
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
Отсюда выразим соотношение среднеквадратичных значений  .
.
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.
Онлайн-калькулятор расчёта реактивного сопротивления
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчитать ёмкость или индуктивность для реактивного сопротивления:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
Активное и реактивное сопротивление
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
С помощью него мы будем смотреть напряжение и силу тока .
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма – это напряжение с генератора Uген , а желтая осциллограмма – это напряжение с шунта Uш , в нашем случае – сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:

Частота 285 Герц:
Частота 30 Килогерц:

Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:

Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.

Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:
Хс – реактивное сопротивление конденсатора, Ом
П – постоянная и приблизительно равна 3,14
С – емкость конденсатора, Фарад
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.

Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка – это полная противоположность конденсатору 
Ну и напоследок давайте еще побалуемся частотой:
С уменьшением частоты сила тока через катушку увеличивается.
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле
ХL – сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
ХL – сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
ХL – сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
ХL – реактивное сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
П – постоянная и приблизительно равна 3,14
L – индуктивность, Генри
Почему не сгорает первичная обмотка трансформатора
П – постоянная и равна приблизительно 3,14
Ну и теперь главный вопрос, который часто задают в личке: “Почему когда я меряю первичную обмотку трансформатора, у меня выдает от 10 Ом и больше в зависимости от трансформатора. На трансформаторных сварочных аппаратах вообще пару Ом! Ведь первичная обмотка трансформатора цепляется к 220 Вольтам! Почему не сгорает обмотка, ведь сопротивление обмотки всего то десятки или сотни Ом, и может случится короткое замыкание!
А ведь и вправду, мощность равна как напряжение помноженное на ток P=IU. То есть через пару секунд от первичной обмотки трансформатора должен остаться уголек.
Дело все в том, что парные обмотки трансформатора представляют из себя катушку индуктивности с какой-то индуктивностью. Получается, что реальное сопротивление обмотки будет выражаться через формулу
поставьте сюда индуктивность, которая в трансформаторах составляет от единицы Генри и получим что-то типа от 300 и более Ом. Но это еще цветочки, ягодки впереди;-)
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или П/2.
Мощность в цепи с реактивными радиоэлементами
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность – это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком “плюс”, а напряжение со знаком “минус”. В итоге плюс на минус дает минус. Получается мощность со знаком “минус”. А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был салабоном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем “плющить” пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно – это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо – это уже другая история для полноценной статьи.
В третий промежуток времени t3 и ток и напряжение у нас со знаком “минус”. Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
RL – это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L – собственно сама индуктивность катушки
С – межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
r – сопротивление диэлектрика и корпуса между обкладками
С – собственно сама емкость конденсатора
ESI (ESL) – эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Резюме
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.
Сопротивление катушки вычисляется по формуле
Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.





